Unit 4 homework 7 proofs review all methods – Unit 4 Homework 7: Proofs Review All Methods delves into the fundamental concepts of mathematical proofs, empowering students with a comprehensive understanding of various techniques for establishing the validity of mathematical statements. This guide provides a thorough overview of direct proof, proof by contradiction, proof by contrapositive, and proof by cases, equipping learners with the necessary tools to tackle complex mathematical challenges.

Throughout this exploration, we will examine real-world examples, break down the intricate steps involved in each method, and highlight their respective strengths and limitations. By engaging with this material, students will not only enhance their mathematical prowess but also cultivate a deeper appreciation for the rigorous nature of mathematical reasoning.

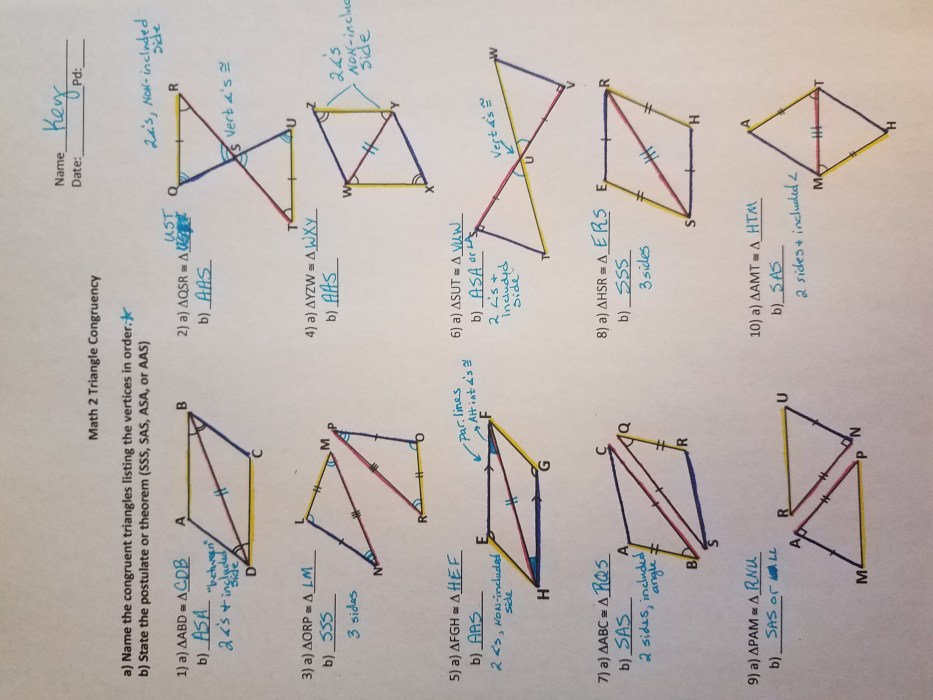
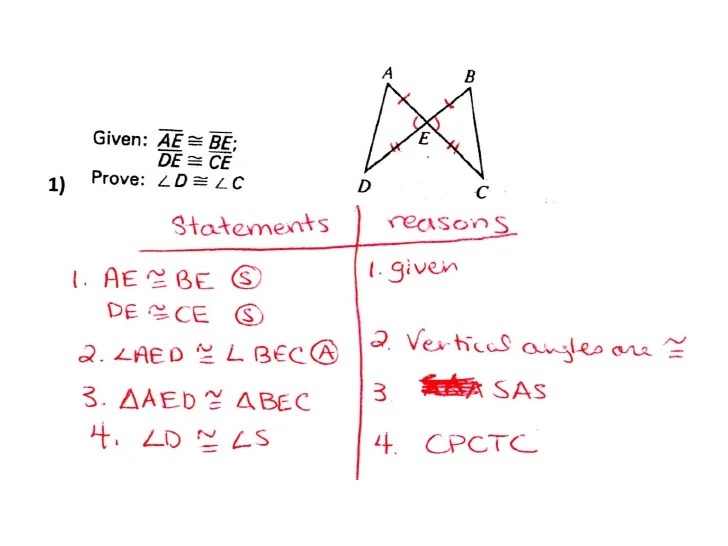
Proof Methods: Unit 4 Homework 7: Unit 4 Homework 7 Proofs Review All Methods

Proofs are essential in mathematics, providing a solid foundation for mathematical statements and theorems. Unit 4 Homework 7 delves into various proof methods, equipping students with the tools to construct rigorous and logical arguments. This article will explore these methods, providing clear explanations and examples to enhance understanding.

Direct Proof, Unit 4 homework 7 proofs review all methods

Direct proof is a straightforward method where the truth of a statement is established directly, without relying on contradictions or indirect reasoning. To construct a direct proof, follow these steps:

• Start with the given assumptions or hypotheses.
• Apply logical reasoning and mathematical properties to deduce new statements.
• Continue the process until you arrive at the desired conclusion.

Example:To prove that if a number is divisible by 3, then the sum of its digits is divisible by 3, use direct proof by:

• Assuming the number is n and it is divisible by 3 (i.e., n = 3k for some integer k).
• Expressing the sum of the digits of n as s = d ₁+ d ₂+ … + d _m, where d _iare the individual digits.
• Showing that s is divisible by 3 by applying the properties of divisibility.

Proof by Contradiction

Proof by contradiction is a method that assumes the negation of the statement to be proven and leads it to a logical contradiction. If a contradiction arises, the original statement must be true.

• Assume the negation of the statement, denoted as ¬P.
• Deduce logical consequences from ¬P.
• Show that these consequences lead to a contradiction, such as a false statement or a violation of a mathematical property.
• Conclude that the original statement P must be true.

Example:To prove that the square root of 2 is irrational, use proof by contradiction by:

• Assuming that √2 is rational, which means it can be expressed as a fraction p/q, where p and q are integers with no common factors.
• Squaring both sides of the equation to get 2 = p ²/q ².
• Multiplying both sides by q ²to get 2q ²= p ².
• Showing that this implies p ²is even, which contradicts the assumption that p and q have no common factors.

Proof by Contrapositive

Proof by contrapositive is a method that proves a statement by proving its contrapositive, which is the logical equivalent with the hypothesis and conclusion swapped.

• State the contrapositive of the original statement.
• Prove the contrapositive using direct proof or other methods.
• Conclude that the original statement is true.

Example:To prove that if n is odd, then n ²is odd, use proof by contrapositive by:

• Stating the contrapositive: If n ²is even, then n is even.
• Assuming n ²is even, which means it is divisible by 2.
• Showing that this implies n is also divisible by 2, using the property that the square of an even number is even.

Proof by Cases

Proof by cases is a method that divides a statement into different cases based on the possible values of a variable or condition.

• Identify the different cases that need to be considered.
• Prove the statement for each case separately.
• Conclude that the statement is true for all cases.

Example:To prove that the function f(x) = x ²is always nonnegative, use proof by cases by:

• Considering two cases: x ≥ 0 and x< 0.
• Showing that f(x) ≥ 0 for x ≥ 0 because the square of a nonnegative number is nonnegative.
• Showing that f(x) ≥ 0 for x< 0 because the square of a negative number is also nonnegative.

Indirect Proof vs. Direct Proof

Indirect proof, also known as proof by contradiction, is a method that assumes the negation of the statement to be proven and leads it to a contradiction. Direct proof, on the other hand, establishes the truth of a statement directly, without relying on contradictions or indirect reasoning.

Table 1: Comparison of Indirect Proof and Direct Proof

Characteristic	Indirect Proof	Direct Proof
Negation	Assumes the negation of the statement.	Does not assume the negation of the statement.
Contradiction	Leads to a contradiction.	Does not involve contradictions.
Validity	Valid if the contradiction is valid.	Valid if the logical reasoning is valid.
Advantages	Can be useful when it is easier to show the negation is false.	Can be more straightforward and intuitive.
Disadvantages	Can be more difficult to find a valid contradiction.	Can be more difficult when there are multiple cases to consider.

FAQ Corner

What is the primary objective of Unit 4 Homework 7?

Unit 4 Homework 7 aims to provide students with a comprehensive review of various proof methods, including direct proof, proof by contradiction, proof by contrapositive, and proof by cases.

Why is it important to understand different proof methods?

掌握多种证明方法对于数学学习至关重要，因为它使学生能够灵活地解决复杂的问题，并根据需要选择最合适的证明技术。